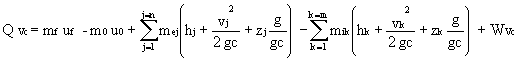Cátedra: Termodinámica
Trabajo
Práctico: Calor Latente
Carrera: Ingeniería
Química
Objetivo: Determinar el calor latente de un líquido
orgánico
Fundamentos teóricos: En este trabajo práctico se determinará
experimentalmente el calor latente de vaporización, utilizando un sistema que
opera en estado uniforme.
Definiciones:
Volumen
de Control: Es un volumen del espacio
que aislamos a través de superficies reales o imaginarias para someterlo a
estudio.
Superficie
de Control: Es aquella superficie,
real o no, que delimita el volumen de control.
El tamaño y la forma del volumen de control
son totalmente arbitrarios, y se lo selecciona de forma de favorecer el
análisis a efectuar.
La masa y/o la energía pueden atravesar las superficies
de control.
Balances de Materia y Energía
Considerando las
propiedades termodinámicas función del tiempo y de la posición en el volumen de
control o el área de intercambio, el Balance de Masa aplicado a un volumen de
control cualquiera puede expresarse a través de la siguiente ecuación:
Balance de Masa
Por su parte el Balance de Energía responde a
la siguiente expresión:
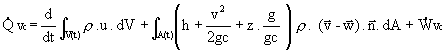
Balance
de Energía
donde:
= caudal calórico intercambiado por el volumen de control.
t = tiempo
r = densidad
V = volumen
u = energía interna
A = áreas de ingreso y/o egreso
= velocidad del flujo material en un punto del
área de ingreso y/o egreso, respecto al marco coordenado de referencia.
= velocidad puntual del volumen de control (o
de sus áreas de ingreso o egreso), respecto al marco coordenado de referencia.
= versor normal al área de ingreso y/o egreso.
h = entalpía
z = cota de altura geométrica
g = aceleración de la gravedad
= potencia intercambiada por
el volumen de control a través de sus áreas móviles.
Proceso en flujo uniforme
Llamaremos de este modo a aquél que resulte de
las siguientes suposiciones:
1.
El volumen de control
permanece fijo con relación al marco coordenado de referencia.
2.
Las propiedades del volumen
de control no son función de la posición pero sí del tiempo.
3.
Las propiedades del medio
ambiente, de los cuales provienen o a los que se descargan las masas del
volumen de control, operan en flujo estable (no se modifican durante el estado
uniforme).
4.
Es aplicable el teorema del
valor medio a las áreas de ingreso y/o egreso de masa.
Bajo estas hipótesis restrictivas
el Balance de masa toma la siguiente forma para n egresos y m ingresos de masa:
Balance de masa
donde
mf = masa final dentro del volumen de control
mo= masa inicial dentro del volumen de control
mej= masa egresada a través del área j durante el proceso
de flujo uniforme analizado
mik= masa ingresada a través del área k durante el proceso
de flujo uniforme analizado
El balance de energía responde a la siguiente ecuación para n egresos
y m ingresos de masa:
Balance de energía
|
|
QVC y WVC representan
respectivamente el calor y el trabajo intercambiado por el volumen de control
con el medio ambiente, durante el proceso de flujo uniforme analizado. A su vez
los subíndices hacen referencia a:
f = Estado final dentro del volumen de control.
o = Estado inicial dentro del volumen de control.
ik = Corriente material de ingreso k.
ej = Corriente material de egreso j.
m = número de áreas de ingreso.
n = número de áreas de egreso.
Esquema del dispositivo
1)
Balón de 2 bocas 9) Depósito del condensado
2)
Manta calefactora 10)
Conexión a la atmósfera
3)
Varivolt 11)
Agitador
4)
Tubo de seguridad 12)
Termómetro
5)
Conducción de vapor 13)
Líquido calorimétrico
6)
Purga del condensado 14)
Aislación
7)
Unión esférica 15) Válvula de 3 vías
8)
Serpentín
1. Técnica
operatoria
a) Determinación
del equivalente en agua del calorímetro
Se introduce el agua en el balón (1); se
cierra una de sus bocas con un tapón que tiene adicionado el tubo de seguridad
(4), mientras que la otra boca se encuentra conectada a la conducción de vapor.
La llave (15) se coloca de manera que quede la conexión abierta a la atmósfera.
Además se introduce una manguera conectada a (15) dentro de un vaso de
precipitado lleno de agua.
Se comienza a calentar el balón mediante un
mechero, ( cuando se utiliza la sustancia orgánicase calentará con manta )
En el recipiente adiabático se coloca agua (la
cantidad necesaria para que el serpentín quede completamente sumergido) y se
unen (8) y (9) (conectado a la atmósfera por (10) al sistema de producción de
vapor a través de la unión esférica (7).
Previamente se colocará grasa para lograr un
buen sello.
El depósito de condensado (9) se debe pesar
previamente a la experiencia, debiéndose limpiar con alcohol y dejar secar,
tratando de tocarlo lo menos posible con las manos antes de pesarlo.
Cuando se ha barrido completamente el aire de
la conducción de vapor (lo cual se comprueba al dejar de salir burbujas del
vaso de precipitado en el cual se ha sumergido la conexión de (15), se deja
circular vapor de 4 a 5 minutos para que la conducción de vapor (5) se
caliente. Durante la puesta en régimen del generador se debe purgar
periódicamente a través de (6) el condensado formado en (5).
Simplemente se comienza a agitar el fluido
calorimétrico, y se comienza a medir la temperatura cada 30 seg. durante 4 o 5
minutos.
Cuando ésta se halla estabilizada, se conecta
mediante la llave (15) el sistema productor de vapor al conjunto
serpentín-depósito.
Se hacen mediciones de la temperatura en el
calorímetro cada 30 seg. y se deja circular vapor hasta que se observa un salto
de temperatura en el calorímetro de 5ºC. Luego se apaga el mechero y se conecta
la llave (15) a la atmósfera. Se siguen tomando lecturas de temperatura hasta
que ésta tienda a estabilizarse. Desconectar (8) y (9) de (7), sacarlos del
calorímetro y soplar el serpentín de manera de hacer caer en el depósito el
condensado que haya quedado retenido.
Secar el depósito, taparlo con el tapón de
goma y pesarlo. Por diferencia de
pesada se obtendrá la masa de agua condensada.
Con los valores de Temperatura vs tiempo se
construirá la gráfica que permitirá obtener el salto de temperatura corregido (D Tc)
Cálculos y resultados
a1) Confeccionar la siguiente tabla con los valores
observados.
|
q (seg.) |
T(ºC) |
|
|
|
|
|
|
|
|
|
a2) Graficar con los valores anteriores el termograma y obtener el D Tc.
a3) Con el valor anterior y la masa de agua condensada y
recogida en el depósito mi, calcular el equivalente en agua del
calorímetro (E).
La ecuación a
utilizar se puede deducir al aplicar los Balances de masa y de energía para
flujo uniforme a nuestro sistema y suponiendo:
·
Que los términos de
variación de energía mecánica y cinética son despreciables en relación a los
términos entálpicos o de energía interna.
·
Que el sistema
serpentín-depósito está al inicio completamente evacuado (sin aire).
Con las condiciones anteriores:
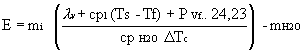
Donde:
E: equivalente en agua del calorímetro (g):
mi: masa de agua condensada (g):
lv: calor latente de vaporización del agua (cal/g):
cp1: calor específico del fluido conocido. (agua) (cal/g
ºC):
Ts: temperatura de saturación del fluido conocido, (agua)
(ºC):
Tfc: temperatura final (corregida) del fluido
calorimétrico. (ºC):
Dtc: salto de temperatura.
(corregido) del fluido calorimétrico, (ºC):
P: presión atmosférica (atm):
vf: volumen específico final del condensado (lt/g):
mH20: masa del agua en el calorímetro (g):
cpH20: calor específico del agua (cal/g ºC):
24,23 cal/lt atm. factor de conversión de unidades.
b) Determinación
del Calor Latente de Vaporización
Terminada
la experiencia para obtener el equivalente se vacía el balón, enjuagando éste y
el depósito con el líquido en estudio.
Los pasos a seguir son similares a los anteriormente descriptos con 2
salvedades:
1 – El Balón se calentará con una manta calefactora (regulada por el
varivolt de manera de no quedar al rojo) para evitar la inflamación del líquido
orgánico en estudio.
2 – Si se utiliza Etanol como fluido orgánico el salto de temperatura
a alcanzar en el termograma deberá ser de aproximadamente 2,5ºC.
Cálculos y resultados
b1) Confeccionar la siguiente tabla con los valores
observados:
|
q (seg) |
T(ºC) |
|
|
|
|
|
|
|
|
|
b2) Graficar con los valores anteriores el termograma y obtener el Dtc.
b3) Con el valor anterior y la masa de agua condensada y
recogida en el depósito mi, calcular el calor latente de
vaporización del fluido orgánico.
La ecuación a utilizar posee las mismas
hipótesis implícitas que la utilizada al evaluar el equivalente.
Donde:
lv: Calor latente de vaporización del líquido (cal/g):
mH20: masa del agua en el calorímetro (g).
E: equivalente en agua del calorímetro (g):
cpH20: calor específico del agua (cal/g ºC):
cpH20: calor específico del agua (cal/g ºC):
cpl: calor específico del líquido orgánico (cal/g ºC):
mi: masa del líquido orgánico condensado (g):
Dtc: salto de temperatura.
(corregido) del fluido calorimétrico (ºC):
cpH20: calor específico del fluido calorimétrico (cal/g
ºC):
Ts: temperatura de saturación del fluido orgánico(agua)
(ºC):
Tfc: temperatura final (Corregida) del fluido calorimétrico
(ºC):
P: presión atmosférica (atm):
vf: volumen específico final del condensado (l/g):
Cuestionario
1 – Obtenga las ecuaciones generales de los Balances de masa y energía
y a partir de allí las ecuaciones para estado uniforme, utilizando las
simplificaciones adecuadas.
2 – A partir del Balance de Energía para estado uniforme, obtenga las
expresiones utilizadas para evaluar E, y lv.
3 – De las suposiciones realizadas en el trabajo práctico, ¿cuáles son
las que introducen mayor error?
Bibliografía
·
Van Wylen y Sonntag.
Termodinámica.
·
Balzhizer-Samuels-Eliassen.
Termodinámica Química para Ingenieros.
·
M.W. Zemansky. Calor y Termodinámica.